力扣 2025 年竞赛题
2025-08
第462场周赛(20250810)
3643. 垂直翻转子矩阵
Details
给你一个 m x n 的整数矩阵 grid,以及三个整数 x、y 和 k。
整数 x 和 y 表示一个 正方形子矩阵 的左上角下标,整数 k 表示该正方形子矩阵的边长。
你的任务是垂直翻转子矩阵的行顺序。
返回更新后的矩阵。
示例 1:
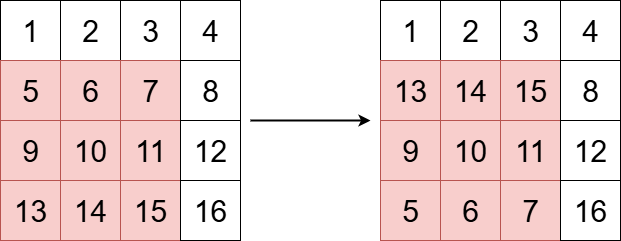
输入: grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], x = 1, y = 0, k = 3
输出: [[1,2,3,4],[13,14,15,8],[9,10,11,12],[5,6,7,16]]
解释:
上图展示了矩阵在变换前后的样子。
示例 2:

输入: grid = [[3,4,2,3],[2,3,4,2]], x = 0, y = 2, k = 2
输出: [[3,4,4,2],[2,3,2,3]]
解释:
上图展示了矩阵在变换前后的样子。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 1000 <= x < m0 <= y < n1 <= k <= min(m - x, n - y)
根据题意,交换的行是[x, x+k-1],交换的列是[y, y+k-1]。
循环列,使用双指针交换左指针和右指针。
初始化左指针left = x,right = x+k-1,循环知道left >= right.
(现在写代码有很多的坑,自己没有想明白,就开始写,很多地方要用右指针,结果写的是k,导致错误。)
class Solution {
public int[][] reverseSubmatrix(int[][] grid, int x, int y, int k) {
// 交换对应的数就要用双指针
// 先循环列
for (int j = y; j < y + k; j++) {
// 双指针交换
int left = x, right = x + k - 1;
while (left < right) {
int t = grid[left][j];
grid[left][j] = grid[right][j];
grid[right][j] = t;
left++;
right--;
}
}
return grid;
}
}3644. 排序排列
Details
给你一个长度为 n 的整数数组 nums,其中 nums 是范围 [0..n - 1] 内所有数字的一个 排列 。
你可以在满足条件 nums[i] AND nums[j] == k 的情况下交换下标 i 和 j 的元素,其中 AND 表示按位与操作,k 是一个非负整数。
返回可以使数组按 非递减 顺序排序的最大值 k(允许进行任意次这样的交换)。如果 nums 已经是有序的,返回 0。
排列 是数组所有元素的一种重新排列。
示例 1:
**输入:**nums = [0,3,2,1]
**输出:**1
解释:
选择 k = 1。交换 nums[1] = 3 和 nums[3] = 1,因为 nums[1] AND nums[3] == 1,从而得到一个排序后的排列:[0, 1, 2, 3]。
示例 2:
**输入:**nums = [0,1,3,2]
**输出:**2
解释:
选择 k = 2。交换 nums[2] = 3 和 nums[3] = 2,因为 nums[2] AND nums[3] == 2,从而得到一个排序后的排列:[0, 1, 2, 3]。
示例 3:
**输入:**nums = [3,2,1,0]
**输出:**0
解释:
只有当 k = 0 时,才能进行排序,因为没有更大的 k 能够满足 nums[i] AND nums[j] == k 的交换条件。
提示:
1 <= n == nums.length <= 1050 <= nums[i] <= n - 1nums是从0到n - 1的一个排列。
说实话,这道题目还是很好理解的,但是现在我连题解都看不懂。
就是求能满足 nums[i] AND nums[j] = k的最大k值。
解题时需要注意的点:
- 元素是从0到n-1,所以说,之后的有序数组满足nums[i] = i
- 是否一定有解,k = 0 ?
class Solution {
public int sortPermutation(int[] nums) {
int ans = -1;
for(int i =0;i<nums.length;i++){
int x = nums[i];
if(i!=x){
ans &= x;
}
}
return Math.max(ans, 0);
}
}2025-04
第 444 场周赛(20250406)
3507. 移除最小数对使数组有序 I
Details
给你一个数组 nums,你可以执行以下操作任意次数:
- 选择 相邻 元素对中 和最小 的一对。如果存在多个这样的对,选择最左边的一个。
- 用它们的和替换这对元素。
返回将数组变为 非递减 所需的 最小操作次数 。
如果一个数组中每个元素都大于或等于它前一个元素(如果存在的话),则称该数组为非递减。
示例 1:
输入: nums = [5,2,3,1]
输出: 2
解释:
- 元素对
(3,1)的和最小,为 4。替换后nums = [5,2,4]。 - 元素对
(2,4)的和为 6。替换后nums = [5,6]。
数组 nums 在两次操作后变为非递减。
示例 2:
输入: nums = [1,2,2]
输出: 0
解释:
数组 nums 已经是非递减的。
提示:
1 <= nums.length <= 50-1000 <= nums[i] <= 1000
面临的问题:
如何将计算出来的值在赋值到原数组上,比如nums=[5,2,3,1],如何将3+1=4的值放入数组?
- 通过使用List的api, remove(lit, index)来实现
如何找到最小的靠左的数对?比如nums=[5,2,3,1],如何确定3+1是最小的?
- 每次循环,将最小的数对记录下来。
class Solution {
public int minimumPairRemoval(int[] nums) {
List<Integer> newnums = new ArrayList<>();
for (int x : nums) {
newnums.add(x);
}
int ans = 0;
// 循环判断
while (!hasSort(newnums)) {
int index = ansIdx(newnums);
int sum = newnums.get(index) + newnums.get(index + 1);
newnums.remove(index + 1);
newnums.set(index, sum);
ans++;
}
return ans;
}
// 判断数组是否有序
boolean hasSort(List<Integer> nums) {
if (nums.size() == 1) {
return true;
}
for (int i = 0; i < nums.size() - 1; i++) {
if (nums.get(i) > nums.get(i + 1)) {
return false;
}
}
return true;
}
// 返回最小数对的下标
int ansIdx(List<Integer> nums) {
int minvalue = nums.get(0) + nums.get(1);
int minindex = 0;
for (int i = 1; i < nums.size() - 1; i++) {
int tmp = nums.get(i) + nums.get(i + 1);
if (tmp < minvalue) {
minvalue = tmp;
minindex = i;
}
}
return minindex;
}
}3510. 移除最小数对使数组有序 II
两种方法:两个有序集合 / 懒删除堆+数组模拟双向链表(Python/Java/C++/Go)
2025年05月
3541. 找到频率最高的元音和辅音
统计一个数组来记录每个字符出现的次数,然后分别求元音字符的最大次数和辅音字符的最大次数
class Solution {
public int maxFreqSum(String s) {
List<Character> vowels = Arrays.asList('a', 'e', 'i', 'o', 'u');
int[] ch = new int[26];
for(int i = 0;i<s.length();i++){
// 'a' 的ascll是97
ch[s.charAt(i) - 97] += 1;
}
int maxy = 0,maxf = 0;
for(int i = 0;i<ch.length;i++){
// int -> char
char c = (char)(i + 97);
if(vowels.contains(c)){
maxy = Math.max(maxy, ch[i]);
}else{
maxf = Math.max(maxf, ch[i]);
}
}
return maxf +maxy;
}
}class Solution {
public int maxFreqSum(String s) {
List<Character> ch = Arrays.asList('a', 'e', 'i', 'o', 'u');
int[] y = new int[26], f = new int[26];
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (ch.contains(c)) {
y[c - 97] += 1;
} else {
f[c - 97] += 1;
}
}
int ans = 0;
Optional<Integer> mx1 = Arrays.stream(y).boxed().max(Integer::compare);
Optional<Integer> mx2 = Arrays.stream(f).boxed().max(Integer::compare);
if (mx1.isPresent()) {
ans += mx1.get();
}
if (mx2.isPresent()) {
ans += mx2.get();
}
return ans;
}
}3542. 将所有元素变为 0 的最少操作次数
class Solution {
public int minOperations(int[] nums) {
if(nums.length == 0)
return 0;
int ans = 0;
while(!isOver(nums)){
int[] con = minNum(nums);
nums = modifyNum(nums, con);
ans++;
}
return ans;
}
public boolean isOver(int[] nums){
for(int x: nums){
if(x != 0){
return false;
}
}
return true;
}
public int[] minNum(int[] nums){
// 找到最小的数和数组下标
int cnt = -1;
int min = 0;
int mx = nums.length;
// 滑动窗口?
return new int[]{cnt, min, mx};
}
public int[] modifyNum(int[] nums, int[] con){
// 修改先有的数组
for(int i = con[1];i<=con[2];i++){
if(i > nums.length){
break;
}
nums[i] = 0;
}
return nums;
}
}2025年04月
第 154 场双周赛
Q1. 使数组和能被 K 整除的最少操作次数
给你一个整数数组
nums和一个整数k。你可以执行以下操作任意次:
- 选择一个下标
i,并将nums[i]替换为nums[i] - 1。返回使数组元素之和能被
k整除所需的最小操作次数。
就是求数组和sum能被k整除需要执行的最小操作次数。
class Solution {
public int minOperations(int[] nums, int k) {
int sum = 0;
for (int x : nums) {
sum += x;
}
int cnt = 0;
while (sum % k != 0) {
// -1
sum--;
cnt++;
}
return cnt;
}
}class Solution {
public int minOperations(int[] nums, int k) {
// 求和取模
// 分类讨论,如果s就是k的倍数,就不用操作
// 如果 s % k == 1, 那么操作一次,如果等于2那么操作两次
// 太强了,直接将题目转化成求和取余数
return Arrays.stream(nums).sum() % k;
}
}Q2. 不同 XOR 三元组的数目 I
给你一个长度为
n的整数数组nums,其中nums是范围[1, n]内所有数的 排列 。XOR 三元组 定义为三个元素的异或值
nums[i] XOR nums[j] XOR nums[k],其中i <= j <= k。返回所有可能三元组
(i, j, k)中 不同 的 XOR 值的数量。排列 是一个集合中所有元素的重新排列。
就是分类讨论,推倒出来的公式。
当n=1时,只有1,个数为1
当n=2时,只有1,2,个数为2
当n=3时,只有0,1,2,3,个数为4个
当n=4时,4的二进制100, 有0 ~7 一共8个数
API:
Integer.toBinaryString(n); 计算n的二进制字符串
String s = Integer.toBinaryString(8); // s = 1000
int len = s.length(); // len = 4Integer.numberOfLeadingZeros(n); 计算n二进制无符号最高有效为前面0的个数
int i = Integer.numberOfLeadingZeros(8); // i = 28class Solution {
public int uniqueXorTriplets(int[] nums) {
// n>=1
int n = nums.length;
if (n <= 2) {
return n;
}
// 求长度n的二进制位数
String s = Integer.toBinaryString(n);
int len = s.length();
// 然后用n的二进制位数来求解,手动推出来的公式
// 当n>2的时候,xor值的数量就是: 二进制位数能表示的最大数+1
int cnt = 0;
for (int i = 0; i < len; i++) {
cnt += Math.pow(2, i);
}
return cnt + 1;
}
}class Solution {
public int uniqueXorTriplets(int[] nums) {
int n = nums.length;
// return n <= 2 ? n : (int) Math.pow(2, 32 - Integer.numberOfLeadingZeros(n));
// Integer.numberOfLeadingZeros(n); 高效的计算出无符号整数最高有效位前面0的个数。
return n <= 2?n: 1 << (32 - Integer.numberOfLeadingZeros(n));
}
}3514. 不同 XOR 三元组的数目 II
给你一个整数数组
nums。XOR 三元组 定义为三个元素的异或值
nums[i] XOR nums[j] XOR nums[k],其中i <= j <= k。返回所有可能三元组
(i, j, k)中 不同 的 XOR 值的数量。
优化三重循环到二重循环。
class Solution {
public int uniqueXorTriplets(int[] nums) {
int mx = 0;
for (int x : nums) {
mx = Math.max(mx, x);
}
// 为什么要做这个操作?
// 求1-n时最多的个数
int u = 1 << (32 - Integer.numberOfLeadingZeros(mx));
boolean[] has = new boolean[u];
for (int i = 0; i < nums.length; i++) {
for (int j = i; j < nums.length; j++) {
has[nums[i] ^ nums[j]] = true;
}
}
boolean[] has3 = new boolean[u];
for (int xy = 0; xy < u; xy++) {
if (!has[xy]) {
continue;
}
for (int z : nums) {
has3[xy ^ z] = true;
}
}
int ans = 0;
for (boolean b : has3) {
if (b) {
ans++;
}
}
return ans;
}
}第 153 场双周赛
还没想好以什么形式记录周赛的题目,暂时每场周赛一个文件吧。
记录做题过程中的思考的问题。
Q1. 字符串的反转度
给你一个字符串s,计算其反转度。
反转度的计算方法如下:
1.对每个字符,将其在反转字母表中的位置('a'=26, 'b'=25...'z'=1),与其字符串中的位置(下标从1开始)相乘。
2.将这些乘积加起来,就得到了字符串中所有字符的和。
返回反转度。
就是用反转字母表中字符的位置 * 字符的位置之和。
在解题的时候,想不到如何维护字母表,就用map来维护了,但是后更好的方式,就是 26 - (s.charAt(i)-'a')就是字符在字母表中的位置。
class Solution {
public int reverseDegree(String s) {
// 主要是维护字母表
int res = 0;
for (int i = 0; i < s.length(); i++) {
int reverse = 26 - (s.charAt(i) - 'a');
res += reverse * (i + 1);
}
return res;
}
}©leetcodeclass Solution {
public int reverseDegree(String s) {
// 主要是维护字母表
int ans = 0;
for (int i = 0; i < s.length(); i++) {
int cnt = (('z' - s.charAt(i)) + 1) * (i + 1);
ans += cnt;
}
return ans;
}
}遇到的问题:
1、a z的ascll码是多少?
- a 97, z 122, A 65, Z 90
2、java中如何将ascll与字符进行转换?
// 将数字转成字符 int num = 97; char x = (char) num; // sout -> x = a // 将字符转成数字 int s = x; // sout -> s = 97
3、java中将的api
- s.toCharArray(), s.charAt(idx)
Q2. 操作后最大活跃区段数 I
给你一个长度为 n 的二进制字符串 s,其中:
'1'表示一个 活跃 区段。'0'表示一个 非活跃 区段。
你可以执行 最多一次操作 来最大化 s 中的活跃区段数量。在一次操作中,你可以:
- 将一个被
'0'包围的连续'1'区块转换为全'0'。 - 然后,将一个被
'1'包围的连续'0'区块转换为全'1'。
返回在执行最优操作后,s 中的 最大 活跃区段数。
**注意:**处理时需要在 s 的两侧加上 '1' ,即 t = '1' + s + '1'。这些加上的 '1' 不会影响最终的计数。
class Solution:
def maxActiveSectionsAfterTrade(self, s: str) -> int:
ans = mx = cnt = 0
pre0 = -inf
for i, b in enumerate(s):
cnt += 1
if i == len(s) - 1 or b != s[i + 1]:
if b == "1":
ans += cnt
else:
mx = max(mx, pre0 + cnt)
pre0 = cnt
cnt = 0
return ans + mxQ4. 操作后最大活跃区段数 II
给你一个长度为 n 的二进制字符串 s ,其中:
'1'表示一个 活跃 区域。'0'表示一个 非活跃 区域。
你最多可以进行一次 操作 来最大化 s 中活跃区间的数量。在一次操作中,你可以:
- 将一个被
'0'包围的连续'1'区域转换为全'0'。 - 然后,将一个被
'1'包围的连续'0'区域转换为全'1'。
此外,你还有一个 二维数组 queries,其中 queries[i] = [li, ri] 表示子字符串 s[li...ri]。
对于每个查询,确定在对子字符串 s[li...ri] 进行最优交换后,字符串 s 中 可能的最大 活跃区间数。
返回一个数组 answer,其中 answer[i] 是 queries[i] 的结果。
注意
- 对于每个查询,仅对
s[li...ri]处理时,将其看作是在两端都加上一个'1'后的字符串,形成t = '1' + s[li...ri] + '1'。这些额外的'1'不会对最终的活跃区间数有贡献。 - 各个查询相互独立。